The following article by Charles Woods appeared in the June 1996 Bulletin. Charles Woods is a retired engineer who lives in Ridgecrest, California. He has been a SCAVM member for ten years.
As an engineer I am more comfortable when I can assign numbers
to things rather than guess and go by trial and error.
There have been a number of articles in the literature on wood
properties and how to measure them, but most of them are not easily
applied by the average violin maker. I have been making simple
tests on all of the wood that I have used since I started making
in 1987 and have accumulated a lot of data that helps me sort
out the good wood from the bad.
Rocky Awalt wrote an article for the SCAVM Bulletin in April, 1985, about his experiences in trying to measure some of the properties that determine good wood; see ref. 1.
One of the most important measurements that you can make to avoid a poor instrument is to measure the cross grain stiffness relative to the longitudinal stiffness of the spruce top. This can be done by making test samples from the wood billet before carving or bending the plate. My experience has been that spruce with a stiffness ratio of greater than 30 to 1 (longitudinal stiffness 30 times stiffer than across the grain) will result in plate that will not tune very well. If you tune your plates using glitter patterns with a sound generator, you will find that this wood will have a low mode 2 frequency and mode 5 will be distorted. Above 50 to 1 ratio, mode 5 may not even be recognizable. I had to scrap a cello top that had a ratio of 51 because it performed so poorly. A top with a ratio of 27 made a tremendous difference. I would have not wasted my time on the first one if I had heeded my own advice! Excellent spruce will have a stiffness ratio of 15 or less. I had a piece of red spruce that measured 11.
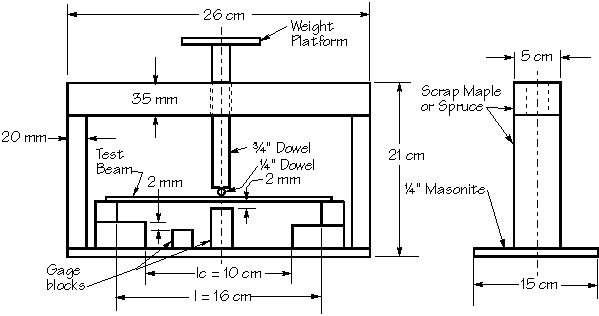
There are several ways to measure the stiffness of a wood sample depending how much information you want on the wood quality. My sample beam tester is shown in the sketch below:

The beam samples are laid across the support blocks and calibrated weights are added to deflect the beam until the gage block will just slide under. I use the 10 cm spacing for the cross grain beam. If you make your test beams exactly the same dimensions and use the same support length, the weights required to bend the beams an equal amount will represent the stiffness of each and the ratio of the stiffness will be Rs = W/Wc, where Wc is the cross grain beam weight. You could also use the same weight on each beam and measure the deflection with a dial indicator.
My method is to bend the beams exactly 2 mm using the gage block and measuring the beam dimensions accurately. Using the simply supported beam deflection formula and solving for E, the modulus of elasticity, we have:
E = W l3/ 4bt3y
where:
W = weight applied
l = beam length between
supports
b = beam width
t = beam thickness
y = deflection (2 mm)
The stiffness ratio is then, E / Ec = Rs.
The speed of sound in both directions in the wood, which is a very important quality parameter, can be calculated once you have determined E and Ec.
IMPORTANT: In the beam formula above, the distance between the supports, l, and the thickness of the beam, t, is a cubed parameter and must be cut or measured very carefully to obtain accurate results. The beam should be measured several places along its length and an average thickness determined.
If you have a balance scale that weighs accurately to milligrams, you can calculate the density of the wood using the dimensions you have measured:
Density, d = w / b t L
where:
w = beam weight
t = beam thickness
L = beam length (not
distance between supports)
b = beam width
We are trying to find wood that is light and stiff, and since the speed of sound is a function of stiffness and density, it is another measure of wood quality. Speed of sound, C = sqrt (E g / d) (g is the gravitational constant).
The article in reference 2 suggests a single number of overall quality using all of these parameters plus the damping factor. Since I don’t have the equipment to measure damping, I have simplified the formula to:
“Quality factor” Q = sqrt(C × Cc) / d where C and Cc are the speed of sound longitudinally and across the grain, and d is the density of the wood. A Q of 6 or more represents very good wood. Longitudinal speed of sound in spruce will vary between 5000 and 6000 meters per second (m/s). Maple will be 4000 to 5000 m/s.
A word about dimensions: you have to be consistent in the use of metric or English units in the formulas for the numbers to make sense. The following are the units to use for each parameter if you are working in the metric system:
Beam length, L;
width, b; thickness, t; and deflection, y — centimeters
Distance between supports,
l — centimeters
Weight to deflect the
beam, W — kilograms
Beam weight, w —
grams
Density, d = 1000 w / b t L (kilograms / cubic meter)
Modulus of elasticity, E =W l3 /4 b t3 y (kg / sq. cm)
Speed of sound, C = sqrt (498,070 E / d) (meters/sec.)
A few practical suggestions: I make my sample beams about 2 mm thick for the longitudinal grain and 4 mm thick for the cross grain. The beams are about 25 mm wide. I use two sets of supports for the beam tests; l = 100 mm for the cross grain and 160 mm for the longitudinal. The beams can be any length, as long as they are longer than the support length. It is more accurate to measure the density using a larger block of the wood, since the beams will weigh less than 10 grams, but if you have a very accurate weighing balance, use the beams.
If any of you have done work similar to this, I would like to hear from you—also if you have questions about any of this that is unclear.
Ref. 1. Awalt, Rocky “Violin Top Wood Cross Grain
Stiffness Considerations.” SCAVM Bulletin, vol. 21 April,
1985.
Ref. 2. Meyer, Hajo G. “A Practical Approach To The Choice
of Tone Wood For Instruments of The Violin Family." Catgut
Acoustical Society, vol. 2 no. 7 (series II) May, 1995.
Ref. 3. Schelling, J. C. “Wood for Violins.” Catgut
Acoustical Society, no. 37, May, 1982.
Mr. Woods' E-mail address is woods@ridgecrest.ca.us.
All Bulletin articles are copyrighted ©1997 by the Southern California Association of Violin Makers. Contact Bulletin editor John Gilson, at the address given on our home page, for permission to reproduce Bulletin material.
Return to home page of the Southern California
Association of Violin Makers .